1.동적계획법(Dynamic Programming, DP)
전체 문제를 작은 부분 문제로 나누어 해결하는 방법
동적계획법의 대표적인 예인 피보나치 수열을 통해 개념을 살짝 이해해보자.
피보나치 수열은 다음과 같다.
1,1,2,3,5,8,13,21,...
다음과 같이 N번째 값은 N-1번째 값과 N-2번째 값이 더해져서 만들어진다는 규칙이 있다.
그럼 이것을 점화식으로 표현해보면 F(N)=F(N-1)+F(N-2)와 같다.
def fibo(n):
if n==1:
return 1
elif n==2:
return 1
else:
return fibo(n-2)+fibo(n-1)
위 코드대로 실행해보면 성공적으로 피보나치 수열이 구해지는 것을 볼 수 있다. 근데 문제점이 있다. 매개변수의 값이 너무 커지면 실행시간이 너무 오래걸린다. 위 코드대로 피보나치 수열이 구해지는 과정을 생각해보면 그 이유를 알 수 있다. 바로 중복계산때문이다.
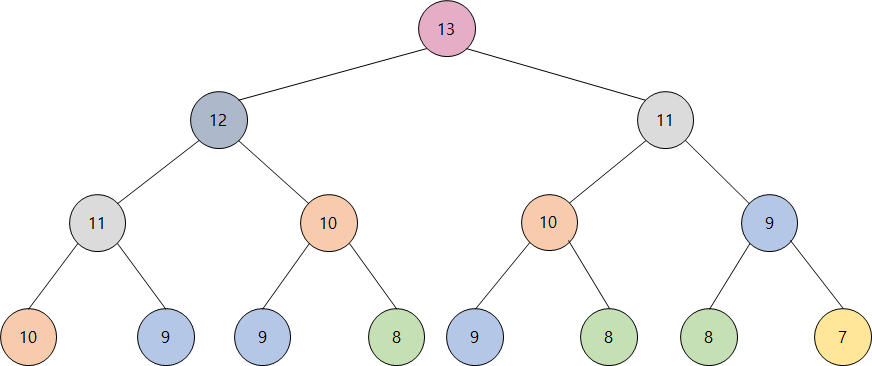
위와 같이 중복이 많이 발생함을 알 수 있다. 그렇다면 중복이 발생할 것들을 미리 계산해 배열에 저장해 놓고 사용하면 실행 시간을 많이 단축할 수 있을 것이다. 물론 메모리를 차지하겠지만!
llist=[0]*100
def fibo2(n):
if n==1:
return 1
elif n==2:
return 1
elif llist[n]!=0:
return llist[n]
else:
llist[n]=fibo2(n-1)+fibo2(n-2)
return llist[n]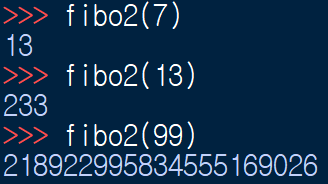
def fibo3(n):
a,b=0,1
for i in range(n-1):
a,b=b,a+b
return b

1-1.동적계획법 접근 방법
1)해를 분석하여 부분 문제로 분할한다.
2)부분 문제의 해로 큰 문제의 해를 표현한다.(점화식으로 표현)
3)적당한 순서대로 table을 채운다.
4)table에서 해를 계산한다.
1-2.구현방식
1)Top-Down
큰 문제를 부분 문제로 나누고 재귀적으로 호출하여 문제를 해결하는 방식
이 방식 구현을 위해 메모이제이션(Memoization)기법을 사용한다.
※메모이제이션(Memoization)
함수의 값을 계산한 뒤 계산된 값을 배열에 저장하는 방식입니다. 이러한 메모이제이션은 필요할 때마다 함수를 다시 호출하지 않고 값을 빠르게 가져올 수 있습니다.
Top-Down방식은 큰 문제를 해결하기 위해서 필요한 부분 문제들만을 계산하므로 특정한 경우 Botton-Up방식보다 빠르게 동작할 수 있다. 하지만 재귀함수를 통해 구현되므로 함수 호출에 대한 오버헤드(함수를 지나치게 많이 호출할 경우, 실행속도가 느려질 수 있음)가 발생할 수 있다.
2)Botton-Up
부분 문제들을 미리 계산해 놓고, 이 문제들을 모아 큰 문제를 해결하는 방식
Botton-Up방식은 반복문을 통해 구현되는데, Top-Down방식에 비해서 시간 및 메모리의 최적화가 편리하다. 하지만 큰문제 해결을 위해서 모든 부분 문제들을 해결해야한다는 단점이 있다.
->쉽게 말하면 for문을 통해 미리 필요한 값들을 구하는 과정?이라고 생각하면 된다.
1-3.대표적인 동적 계획법 문제들
1)피보나치 수열
2)Coin Change Problem
3)LCS
이제 대표적인 동적 계획법 문제들을 직접 풀어보자.
피보나치 수열 문제는 개념을 다루며 위에서 풀었으니 2번부터 접근해보자.
2)Coin Change Problem
문제
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 231보다 작다.
예제 입력 1
3 10
1
2
5
예제 출력 1
10
위의 예제를 바탕으로 알고리즘을 설명해보자.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 2 | 3 |
위 표는 각 동전으로 해당 금액을 만드는 방법을 의미한다.
1번째 행은 1원짜리 동전으로 해당 금액을 만드는 방법, 2번째 행은 1원과 2원짜리 동전으로 해당 금액을 만드는 방법, 3번째 행은 1원,2원, 그리고 5원짜리 동전으로 해당 금액을 만드는 방법이다.
2행 4열의 파란색으로 표시한 부분을 이해하여 보자. 4원에서 2원을 빼면 2원이다. 구한 바에 의하면(하늘색으로 표시된 부분) 남은 금액, 즉 2원으로 1원과 2원으로 만드는 방법 수는 2가지이다. 따라서 1원과 2원으로 4원으로 만드는 방법은 2가지이다. 표의 나머지 부분도 같은 논리이다.
#1,2,5
coin=[1,2,5]
table=[0]*10
table[0]=1
def dp(N):
for i in range(len(coin)):
for c in range(coin[i],N+1,1):
print(c)
table[c]+=table[c-coin[i]]
dp(9)
print(table)
3)LCS
문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.
예제 입력 1
ACAYKP
CAPCAK
예제 출력 1
4
부분수열->1)순서가 존재할 것, 2)부분 집합일 것을 만족해야 한다.
| 0 | A | C | A | Y | K | P | |
| 0 | |||||||
| C | 1 | ||||||
| A | 1 | 1 | |||||
| P | 1 | ||||||
| C | 1 | ||||||
| A | 1 | 1 | |||||
| K | 1 |
| 0 | A | C | A | Y | K | P | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| A | 0 | 1 | 1 | 2 | 2 | 2 | 2 |
| P | 0 | 1 | 2 | 2 | 2 | 2 | 3 |
| C | 0 | 1 | 2 | 3 | 3 | 2 | 3 |
| A | 0 | 1 | 2 | 3 | 3 | 3 | 3 |
| K | 0 | 1 | 2 | 3 | 3 | 4 | 4 |

S1='ACAYKP'
S2='CAPCAK'
table=[[0 for i in range(len(S1)+1)] for j in range(len(S2)+1)]
for i in range(len(S1)):
for j in range(len(S2)):
if S1[i]==S2[j]:
table[j+1][i+1]+=(table[j][i]+1)
else:
table[j+1][i+1]=max(table[j+1][i],table[j][i+1])'알고리즘' 카테고리의 다른 글
| [알고리즘]순열, 조합, 부분집합 - Java로 구현하기 (1) | 2024.02.24 |
|---|---|
| [알고리즘]DynamicProgramming (0) | 2022.04.23 |
| [알고리즘]Sorting Algorithm_RadixSort (0) | 2022.04.23 |
| [알고리즘]Sorting Algorithm_HeapSort (0) | 2022.04.23 |
| [알고리즘]깊이/너비 우선 탐색 (0) | 2021.01.16 |