728x90
1.그래프 알고리즘
1-1.그래프
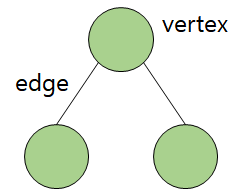
정점(vertex)와 edge로 이루어져 있다. 방향성을 가질 수도 있다.
1-2.파이썬으로 그래프를 표현해보자
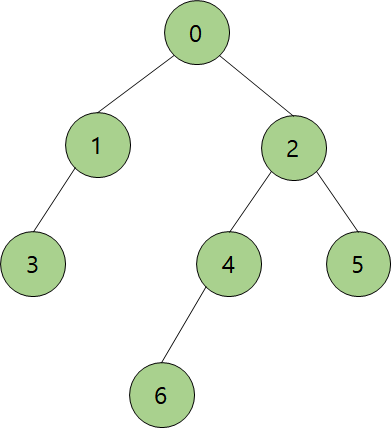
#vertexList: vertex들을 리스트에 전부 넣은 것
#edgeList: edge들을 리스트에 전부 넣은 것
vertexList=['0','1','2','3','4','5','6']
edgeList=[(0,1),(0,2),(1,0),(1,3),(2,0),(2,4),(2,5),(3,1),(4,2),(4,6),(5,2),(6,4)]
adjacencyList=[[] for vertex in vertexList]
for edge in edgeList:
adjacencyList[edge[0]].append(edge[1])
※트리도 그래프의 일종이다-!
깊이 우선 탐색 > 스택, 너비 우선 탐색 > 큐를 이용해 구현할 수 있다.
2.깊이 우선 탐색(DFS)
2-1.코드로 구현
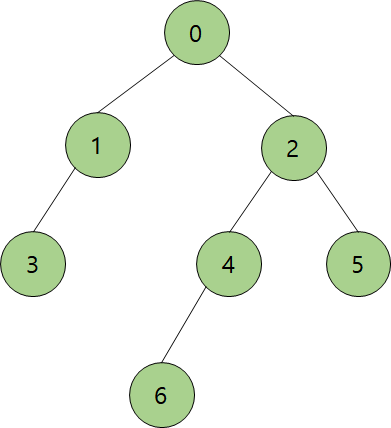
위의 그래프를 깊이 우선 탐색을 통해 탐색해보자.
adj={vertex:[] for vertex in vertexList}
for edge in edgeList:
adj[edge[0]].append(edge[1])
def dfs(graph, root):
visited = []
stack = [root]
while stack:
current=stack.pop()
for neighbor in adj[current]:
if neighbor not in visited:
stack.append(neighbor)
visited.append(current)
return visited
visited = []
def dfs2(graph, root):
stack = [root]
current=stack.pop()
visited.append(current)
for neighbor in adj[current]:
if neighbor not in visited:
dfs2(graph,neighbor)결과를 확인해보자

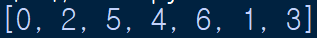
2-2.단계별로 확인해보자.
사실 처음에 코드를 통해서만 이해를 하려고 하니까 너무 어려웠다ㅜㅜㅜ 코린이는 웁니다 흑흑흑
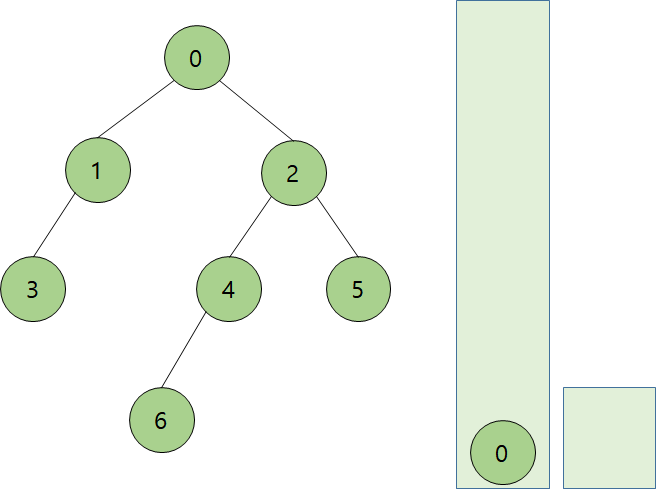
1)첫번째 원소를 스택에 넣는다.
stack = [root]

2)스택에서 원소를 하나 꺼낸다.
current=stack.pop()

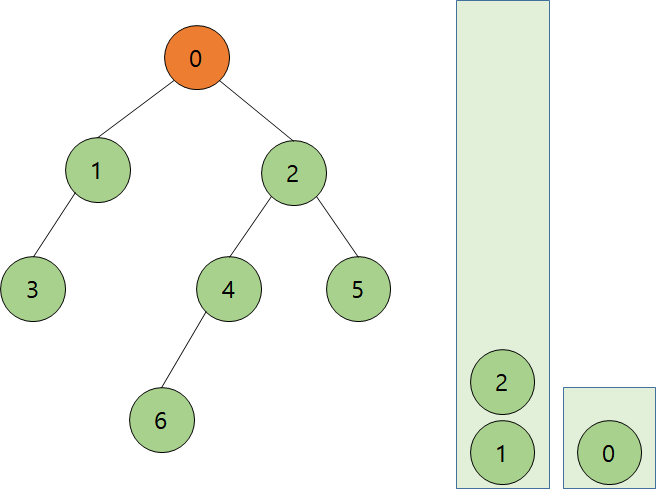
3)원소와 인접한 원소가 이미 방문한 정점이 아니라면 스택에 넣는다. 그리고 현재 원소를 이미 방문한 원소리스트에 넣는다.
for neighbor in adj[current]:
if neighbor not in visited:
stack.append(neighbor)
visited.append(current)4)스택의 원소가 하나도 없을 때까지 위 과정을 반복->while문
3.너비 우선 탐색(BFS)
3-1.코드로 구현
def bfs(graph, root):
visited = []
queue = [root]
while queue:
current=queue.pop()
for neighbor in adj[current]:
if neighbor not in visited:
queue.insert(0,neighbor)
visited.append(current)
return visitedimport queue
def bfs2(adj,start):
visited=[]
tovisit=queue.Queue()
tovisit.put(start)
while not tovisit.empty():
current=tovisit.get()
for vertex in adjacencyList[current]:
if vertex not in visited:
tovisit.put(vertex)
visited.append(current)
return visited결과를 확인해보자

흠 깊이 우선 탐색은 스택을 사용하니까 자식 노드부터 점점 탐색하게 되는 것 같고, 너비 우선 탐색은 반대로 큐를 이용하니까 부모 노드 탐색을 모두 마치고 자식 노드를 방문하게 되는 것 같다-!오호
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘]순열, 조합, 부분집합 - Java로 구현하기 (1) | 2024.02.24 |
|---|---|
| [알고리즘]DynamicProgramming (0) | 2022.04.23 |
| [알고리즘]Sorting Algorithm_RadixSort (0) | 2022.04.23 |
| [알고리즘]Sorting Algorithm_HeapSort (0) | 2022.04.23 |
| [알고리즘]동적 계획법 (0) | 2021.01.18 |